Matematika kelas 8 BAB 1 Pola Bilangan (untuk tanggal 20 Juli 2020)

Assalamu'alaikum warohmatullohi wabarokatuh.

Perkenalkan nama Ibu Lita Yuliyahya. Ibu mengajar matematika di kelas VIII-E, VIII-F, dan VIII-J. Meskipun pembelajaran untuk semester ini kita belum bisa bertatap muka, namun ibu harap siswa-siswi tetap semangat mempelajari materi yang akan ibu sampaikan dan jadikan pembelajaran ini meningkatkan kemandirian dan rasa ingin tahu yang lebih tinggi.

Materi matematika untuk kelas VIII di semester 1 ada lima (5) pokok bahasan, yaitu:
1. Pola Bilangan
2. Sistem Koordinat Kartesius
3. Relasi dan Fungsi
4. Persamaan garis Lurus
5. Sistem Persamaan Linear Dua Variabel

Mudah-mudahan ibu bisa memberikan dan menyampaikan semua materi di tengah keterbatasan waktu ini. Untuk pertemuan sekarang, materi yang akan disampaikan tentang Pola Bilangan.




                                    BAB 1

                                                POLA BILANGAN


Pengertian Pola Bilangan

Definisi pola bilangan matematika adalah susunan dari beberapa angka yang dapat membentuk pola tertentu. Pola bilangan juga bisa diartikan sebagai suatu susunan bilangan yang memiliki bentuk teratur atau suatu bilangan yang tersusun dari beberapa bilangan lain yang membentuk suatu pola.

Macam-Macam Pola Bilangan

Berikut ini jenis pola bilangan dalam matematika dan contohnya:

Pola Bilangan Ganjil

Pengertian pola bilangan ganjil adalah pola bilangan yang terbentuk dari bilangan-bilangan ganjil. Sedangkan pengertian bilangan ganjil adalah suatu bilangan asli yang tidak habis dibagi dua ataupun kelipatannya.

Gambar Pola Bilangan Ganjil


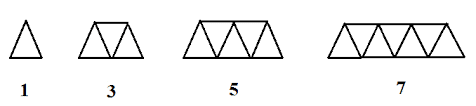
Rumus Pola Bilangan ganjil

1 , 3 , 5 , 7 , . . . , n , maka rumus pola bilangan ganjil ke n adalah:

Un = 2.n - 1

Keterangan: n = banyaknya suku

Contoh Soal Pola Bilangan Ganjil

1 , 3 , 5 , 7 , . . . , ke 12. Berapakah pola bilangan ganjil ke 12 ?

Jawab :

Un = 2.n -1
U12 = 2.12 -1
U12 = 24 -1 = 23


Pola Bilangan Genap

Pengertian pola bilangan genap adalah pola bilangan yang terbentuk dari bilangan-bilangan genap . Bilangan genap adalah bilangan asli yang habis dibagi dua atau kelipatannya .

Pola bilangan genap adalah 2 , 4 , 6 , 8 , . . .

Gambar Pola Bilangan Genap


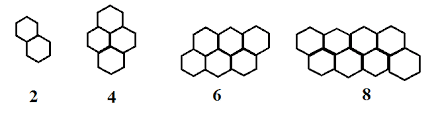
Rumus Pola Bilangan Genap

Berikut pola bilangan genap.

2 , 4 , 6 , 8 , . . . . , n maka rumus pola bilangan genap ke n adalah:

Un = 2n

Contoh Soal Pola Bilangan Genap

2 , 4 , 6 , 8 , . . . ke 12 . Berapakah pola bilangan genap ke 12 ?

Jawab :

Un = 2n
U12 = 2 x 12
U12 = 24


Pola Bilangan Persegi

Pengertian pola bilangan persegi adalah suatu barisan bilangan yang membentuk suatu pola persegi . Pola bilangan persegi adalah 1 , 4 , 9 , 16 , 25 , . . .

Gambar Pola Bilangan Persegi


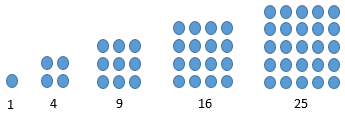
Rumus Pola Bilangan Persegi

1 , 4 , 9 , 16 , 25 , 36 , . . . , n maka rumus untuk mencari pola bilangan persegi ke-n adalah:

Un = n2

Contoh Pola Bilangan Persegi

Dari suatu barisan bilangan 1 , 4 , 9 , 16 , 25 , 36 , . . . ,ke 12 . Berapakah pola bilangan ke 12 dalam pola bilangan persegi ?

Jawab :

Un = n2
U12 = 122
U12 = 144


Pola Bilangan Persegi Panjang

Pengertian pola bilangan persegi panjang adalah suatu barisan bilangan yang membentuk pola persegi panjang . Pola persegi panjang adalah 2 , 6 , 12 , 20 , 30 , . . .

Gambar Pola Bilangan Persegi Panjang

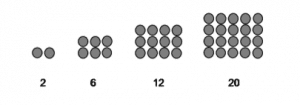
Rumus Pola Bilangan Persegi Panjang

2 , 6 , 12 , 20 , 30 , . . . n , maka rumus pola bilangan persegi panjang ke-n adalah:

Un = n . n + 1

Contoh Soal Pola Bilangan Persegi Panjang

Dari suatu barisan bilangan 2 , 6 , 12 , 20 , 30 , . . . , ke 12 . Berapakah pola bilangan persegi ke 12?

Jawab :

Un = n . n+ 1
U12 = 12 . 12 + 1
U12 = 12 . 13
U12 = 156


Pola Bilangan Segitiga

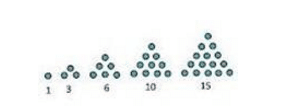
Pengertian bola bilangan segitiga adalah suatu barisan bilangan yang membentuk sebuah pola bilangan segitiga. Pola bilangan segitiga adalah 1 , 3 , 6 , 10 , 15 , . . .

Gambar Pola Bilangan Segitiga

Rumus Pola Bilangan Segitiga

1 , 3 , 6 , 10 , 15 , 21 , 28 , 36 , . . . , ke n . Maka rumus pola bilangan segitiga ke n adalah:

Un = 1/2 n ( n + 1 )

Contoh Soal Pola Bilangan Segitiga

Dari suatu barisan bilangan 1 , 3 , 6 , 10 , 15 , 21 , 28 , 36 , . . . , ke 12 . Berapakah pola bilangan segitiga ke 12?

Jawab :

Un = 1/2 n ( n + 1 )
U12 = 1/2 . 12 (12 + 1)
U12 = 6 (13)
U12 = 78

Pola Bilangan Fibonacci

Pengertian pola bilangan fibonacci adalah suatu bilangan yang setiap sukunya merupakan jumlah dari dua suku di depannya. Pola bilangan Fibonacci adalah 1, 1, 2, 3, 5, 8, 13, 21, 34, ……

Perlu diketahui, 2 diperoleh dari hasil 1 + 1, 3 diperoleh dari hasil 2 + 1, 5 diperoleh dari hasil 3 + 2 dan seterusnya.

Rumus mencari suku ke-n pola bilangan fibonacci adalah Un = Un-1 + Un-2

Gambar Pola Bilangan Fibonacci

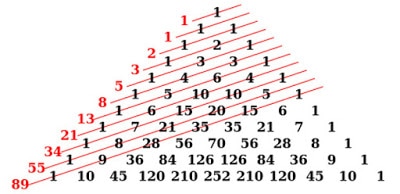
Pola Bilangan Segitiga Pascal

Bilangan pascal ditemukan oleh oleh orang Prancis bernama Blaise Pascal, sehingga dinamakan bilangan pascal. Bilangan pascal adalah bilangan yang terbentuk dari sebuah aturan geometri yang berisi susunan koefisien binomial yang bentuknya menyerupai segitiga.

Di dalam segitiga pascal, bilangan yang terdapat pada satu baris yang sama dijumlahkan menghasilkan bilangan yang ada di baris bawahnya. Jadi, pengertian pola bilangan pascal adalah suatu pola yang tersusun dari beberapa angka berdasarkan rumus: (perhatikan gambar pola bilangan pascal)


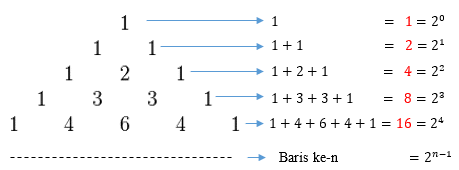
Pola bilangan pascal adalah 1, 2, 4, 8, 16, 24, 32, 64,…..


Pola Bilangan Pangkat Tiga

Pola bilangan pangkat tiga adalah pola bilangan dimana bilangan setelahnya merupakan hasil dari pangkat tiga dari bilangan sebelumnya. Contoh pola bilangan pangkat tiga adalah 2, 8, 512, 134217728, …..

Keterangan : 8 diperoleh dari hasil 2 pangkat tiga, 512 diperoleh dari hasil 8 pangkat tiga, dan seterusnya.


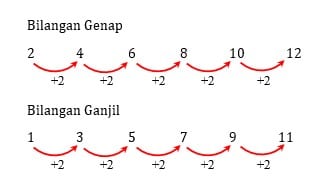
Pola Bilangan Aritmatika

Pengertian pola bilangan aritmatika adalah pola bilangan dimana bilangan sebelum dan sesudahnya memiliki selisih yang sama. Contoh pola bilangan aritmatika adalah 2, 5, 8, 11, 14, 17, ….

Suku pertama dalam bilangan aritmatika disebut dengan awal ( a ) atau U1, sedangkan suku kedua adalah U2 dan seterusnya.

Selisih dalam barisan aritmatika disebut dengan beda dan dilambangkan dengan b.
Karena bilangan sebelum dan sesudahnya memiliki selisih yang sama, 

maka b = U2 – U1 = U3 – U2 = U4 – U3 = U5 – U4 = U6 – U5 = 3
Rumus mencari suku ke-n adalah Un = a + (n -1) b
Rumus mencari jumlah n suku pertama adalah Sn = n/2 (a + Un) atau

 Sn = n/2 (2 a + ( n-1 ) b )

Contoh Pola Bilangan Aritmatika

Pola Bilangan Geometri

Pengertian pola bilangan geometri adalah suatu bilangan hasil perkalian bilangan sebelumnya dengan suatu bilangan yang tetap.

Rumus suku ke-n adalah Un = arn-1

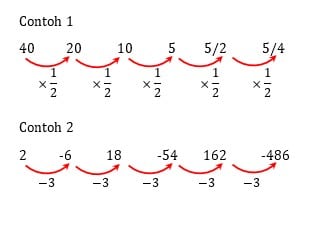
Contoh Pola Bilangan Geometri

Sekian pembahasan materi tentang Pola Bilangan. Untuk soal-soal latihan akan dikirimkan melalui grup whatsapp. Berikut nomor WA ibu 085323385282 apabila ada materi ataupun pertanyaan bisa langsung dihubungi.

Terima kasih.

Wassalamu'alaikum warohmatullohi wabarokatuh.

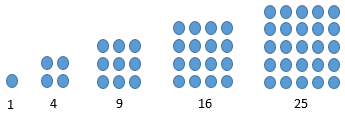
Komentar

Posting Komentar

Postingan populer dari blog ini

MENENTUKAN PERSAMAAN DARI SUATU KONFIGURASI OBJEK (3 AGUSTUS 2020)

Gambar
Materi konfigurasi objek merupakan materi yang masih terdapat dalam bab 1 yaitu Pola Bilangan. MENENTUKAN PERSAMAAN DARI SUATU KONFIGURASI OBJEK        Berikut ini kalian akan diajak untuk mengamati suatu   konfigurasi objek. Setelah mengamati konfigurasi objek tersebut, kalian diajak untuk menggali informasi tentang pola bilangan yang terbentuk, sehingga pada akhirnya kalian bisa membuat persamaan pola bilangan yang kalian temukan.   1. Barisan Aritmatika Derajat Satu Pengertian  Barisan aritmatika  adalah baris yang nilai setiap sukunya didapatkan dari suku sebelumnya melalui  penjumlahan  atau  pengurangan   dengan suatu bilangan. Selisih atau beda antara nilai suku-suku yang berdekatan selalu sama yaitu  b . Nilai suku pertama dilambangkan dengan  a . Untuk mengetahui nilai suku ke-n dari suatu barisan arimatika dapat dihitung dengan rumus berikut.   Barisan aritmatika tersebut dinamakan...
Baca selengkapnya

Operasi hitung pada bilangan pecahan

Gambar
OPERASI HITUNG PADA BILANGAN PECAHAN Siapa di antara kamu yang tahu apa saja operasi hitung dalam Matematika?   Yup ! Operasi hitung dalam Matematika ada lima macam, yaitu penjumlahan, pengurangan, perkalian, pembagian, dan pemangkatan. Ternyata, empat dari lima operasi hitung ini dapat digunakan untuk membantu kita dalam mengoperasikan bilangan pecahan,   lho . Apa saja ya?   Yuk , langsung saja kita simak pembahasannya satu persatu pada artikel di bawah ini! Penjumlahan dan Pengurangan Operasi hitung yang pertama dan kedua adalah penjumlahan dan pengurangan. Ketika kita ingin menjumlahkan atau mengurangkan dua atau lebih pecahan, terdapat beberapa langkah yang harus kita lakukan terlebih dahulu,  nih .  Eits ! kamu  nggak  usah khawatir, langkahnya mudah  kok .  So ,  let’s check this out ! a. Menyamakan penyebut Langkah yang pertama adalah menyamakan penyebut.  Hayo , ada yang masih ingat apa itu penyebut? Ya, penyebut itu adalah...
Baca selengkapnya

DIAGRAM GARIS DAN DIAGRAM LINGKARAN

Gambar
 Pertemuan sebelumnya kita sudah membahas penyajian data dengan diagram batang. Pertemuan hari ini kita membahas tentang penyajian data dengan Diagram Garis dan Diagram Lingkaran. Semangat mmpeljarainya :) b. Diagram Garis Diagram garis biasanya digunakan untuk menyajikan  data yang berkelanjutan/kontinu , seperti jumlah penduduk setiap tahun, jumlah produksi barang setiap tahun, perubahan iklim dan cuaca pada rentang waktu tertentu, dan lain sebagainya. Sesuai namanya, pada diagram garis, data akan digambarkan membentuk garis.  Nah , cara menyajikan data dalam diagram garis hampir sama dengan diagram batang. Hanya langkah akhirnya saja yang berbeda. Kamu hanya perlu menarik garis secara berurut dari titik-titik yang telah disesuaikan dengan data. Kalau data tinggi badan siswa kelas 7A kita buat ke dalam diagram garis, hasilnya akan seperti ini: c. Diagram Lingkaran ( Pie ) Diagram lingkaran biasanya digunakan untuk menyajikan data yang  dapat dikategorikan/dikelompo...
Baca selengkapnya